Số chính phương- Khám phá quy tắc bất thành văn

Trong thế giới toán học đầy mê hoặc, số chính phương luôn ẩn chứa những bí ẩn và sự thú vị thu hút các nhà toán học và cả những người đam mê khám phá. Vậy số chính phương là gì, nó có những đặc điểm gì nổi bật và đóng vai trò quan trọng như thế nào trong toán học? Bài viết này sẽ đưa bạn vào hành trình khám phá bí ẩn của những con số hoàn hảo này, giúp bạn hiểu rõ hơn về số chính phương và vai trò quan trọng của nó trong nhiều lĩnh vực khác nhau.

Số chính phương là gì?

Dưới đây là khái niệm cơ bản, đặc điểm và công thức tính của số chính phương:

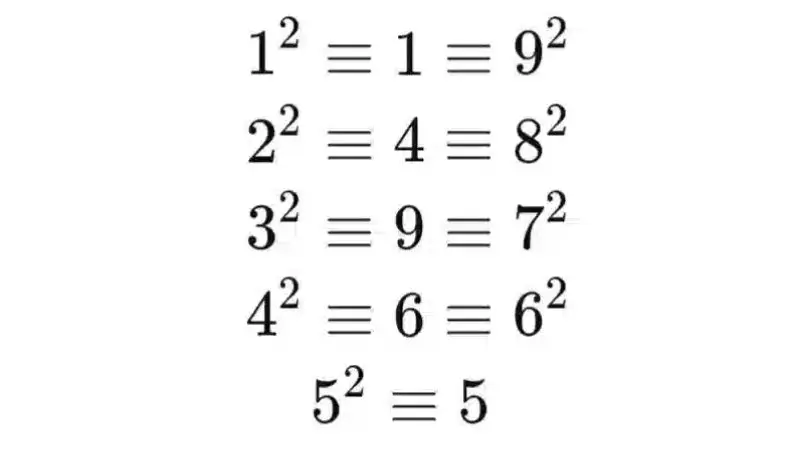
Khái niệm

Số chính phương là một số tự nhiên có thể được biểu diễn dưới dạng bình phương của một số nguyên khác. Hay nói cách khác, số chính phương là số bằng bình phương đúng của một số nguyên.

Ví dụ:

16 là số chính phương vì 16 = 4^2 (bốn bình phương)

25 là số chính phương vì 25 = 5^2 (năm bình phương)

36 là số chính phương vì 36 = 6^2 (sáu bình phương)

Đặc điểm của số chính phương:

Chữ số tận cùng: Chữ số tận cùng của một số chính phương chỉ có thể là 0, 1, 4, 5, 6 hoặc 9.

Phân tích thừa số nguyên tố: Khi phân tích một số chính phương ra thừa số nguyên tố, ta thấy số mũ của mỗi thừa số nguyên tố đều chẵn.

Kiểm tra bằng máy tính: Máy tính cầm tay hoặc máy tính khoa học có chức năng kiểm tra số chính phương.

Công thức tính số chính phương

Với mọi số nguyên n, ta có thể tính số chính phương của n theo công thức: n^2, trong đó n là số nguyên cần tính bình phương.

Ví dụ:

Số chính phương của 7 là 7^2 = 49

Số chính phương của -5 là (-5)^2 = 25

Cách xác định số chính phương

Có nhiều cách để xác định số chính phương, bao gồm:

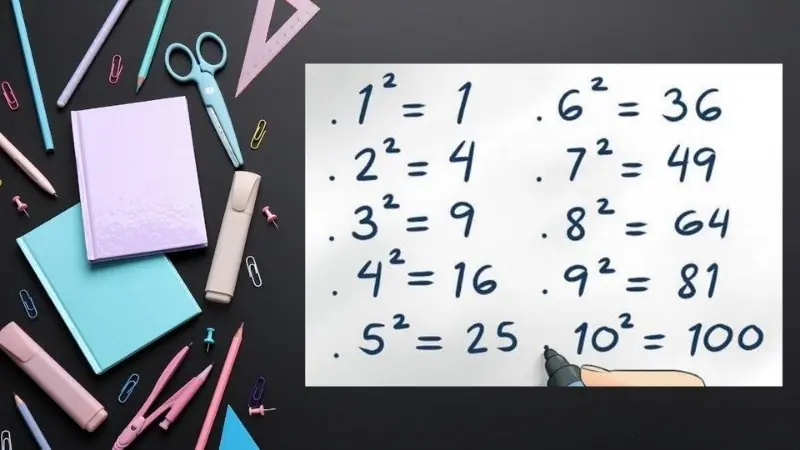
Kiểm tra chữ số tận cùng

Chữ số tận cùng của một số chính phương chỉ có thể là 0, 1, 4, 5, 6 hoặc 9.

Ví dụ:

13 không phải là số chính phương vì chữ số tận cùng là 3.

211 là số chính phương vì chữ số tận cùng là 1.

Phân tích thừa số nguyên tố

Khi phân tích một số chính phương ra thừa số nguyên tố, ta thấy số mũ của mỗi thừa số nguyên tố đều chẵn.

Ví dụ:

100 = 2^2 x 5^2 là số chính phương vì số mũ của mỗi thừa số nguyên tố đều chẵn.

15 = 3 x 5 không phải là số chính phương vì số mũ của thừa số 5 là lẻ.

Sử dụng máy tính:

Máy tính cầm tay hoặc máy tính khoa học có chức năng kiểm tra số chính phương.

Ví dụ:

Trên máy tính casio, bạn có thể bấm SHIFT + 2ndF + √ sau đó nhập số cần kiểm tra. Nếu kết quả là số nguyên, thì đó là số chính phương.

Trên máy tính Windows, bạn có thể mở ứng dụng Máy tính, nhập số cần kiểm tra, sau đó bấm ^2. Nếu kết quả là số nguyên, thì đó là số chính phương.

Công thức

Với mọi số nguyên n, ta có thể tính số chính phương của n theo công thức: n^2, trong đó n là số nguyên cần tính bình phương.

Ví dụ:

Số chính phương của 8 là 8^2 = 64.

Số chính phương của -4 là (-4)^2 = 16.

Một số cách khác

Sử dụng bảng số chính phương: Có sẵn các bảng số chính phương trên internet hoặc trong sách giáo khoa toán học. Bạn có thể tra cứu số cần kiểm tra trong bảng để xem nó có phải là số chính phương hay không.

Sử dụng phương pháp hình học: Số chính phương có thể được biểu diễn bằng diện tích của một hình vuông. Ví dụ, số 9 là số chính phương vì nó bằng diện tích của hình vuông có cạnh dài 3.

Vai trò của số chính phương

Số chính phương đóng vai trò quan trọng trong nhiều lĩnh vực khác nhau, bao gồm:

Toán học

Số học: Số chính phương là một khái niệm cơ bản trong số học, được sử dụng để xây dựng các khái niệm toán học khác như số nguyên tố, số hoàn hảo, số chia hết, …

Đại số: Số chính phương được sử dụng trong nhiều phép toán đại số, như khai căn bậc hai, giải phương trình bậc hai, …

Hình học: Số chính phương được sử dụng để tính diện tích của các hình vuông, hình chữ nhật, …

Lý thuyết số: Số chính phương đóng vai trò quan trọng trong nhiều bài toán lý thuyết số, như chứng minh định lý Fermat, …

Vật lý

Chuyển động của vật thể: Số chính phương được sử dụng để mô tả chuyển động của vật thể rơi tự do, chuyển động ném ngang, …

Lực hấp dẫn: Số chính phương được sử dụng để tính lực hấp dẫn giữa hai vật thể.

Điện từ học: Số chính phương được sử dụng trong các công thức điện từ học, như định luật Ohm, định luật Faraday, …

Khoa học máy tính

Thuật toán: Số chính phương được sử dụng trong nhiều thuật toán, như thuật toán sắp xếp, thuật toán tìm kiếm, …

Mật mã học: Số chính phương được sử dụng trong một số hệ thống mật mã.

Đồ họa máy tính: Số chính phương được sử dụng trong đồ họa máy tính để tính toán các hiệu ứng hình ảnh.

Các lĩnh vực khác

Kinh tế học: Số chính phương được sử dụng trong một số mô hình kinh tế học.

Âm nhạc: Số chính phương được sử dụng trong một số lý thuyết âm nhạc.

Nghệ thuật: Số chính phương được sử dụng trong một số tác phẩm nghệ thuật.

Số chính phương là những con số đặc biệt đóng vai trò quan trọng trong toán học và nhiều lĩnh vực khác nhau. Hiểu rõ về số chính phương là gì giúp chúng ta giải quyết nhiều bài toán phức tạp, phát triển các thuật toán tiên tiến và khám phá những bí ẩn ẩn chứa trong thế giới toán học. Hy vọng những thông tin trong bài viết này đã giúp bạn hiểu rõ hơn về số chính phương và khơi dậy niềm đam mê khám phá toán học trong bạn.